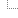expr bit-wise "xor" operator

Arguments must be integers, result is an integer.

Bit n of the result is 1 if bit n of the two arguments differ. Otherwise, bit n of the result is 0.

To evaluate $a^$b when either $a or $b is negative, we make use of the following reasoning:

Case	Result
$a>=0, $b>=0	Bitwise operation
$a>=0, $b<0	$a^$b == ~($a ^ ~$b) Contrapositive law $a^$b == ~($a ^ (-1-$b)) Extended definition of ~ $a^$b == -1-($a ^ (-1-$b)) Extended definition of ~ Since $a and (-1-$b) are both non-negative, the ^ in the last expression can be evaluated in bitwise fashion.
$a<0, $b>=0	Commute to ($b^$a) and evaluate as above.
$a<0, $b<0	$a^$b == (~$a) ^ (~$b) Contrapositive law $a^$b == (-1-$a) ^ (-1-$b) Extended definition of ~ Since (-1-$a) and (-1-$b) are both positive, the ^ in the last expression can be evaluated in bitwise fashion.

Examples edit

% expr 0b010 | 0b000
2

[So, what do I need to add to this example so the result is binary as well? Some sort of format - but I don't see a binary conversion sequence in the docs...] RS: See for instance to.binary

---