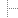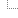Richard Suchenwirth 2002-12-01 - Here are some little pieces that don't deserve a page of their own yet.

---

A sum to get e edit

Reading "What is J?" (the ASCIIfied successor to APL, see Playing APL), one nice example was how to approximate the Euler number e:

 +/ % ! i. 9

which in more conventional math notation is

 _8_
 \     1
  >   ---
 /__   i!
 i=0

Too lazy to start and reimplement J in Tcl, I decided to express this in Tcl as natural as possible:

 proc Sum {itName from to body} {
    upvar 1 $itName it
    set res 0
    for {set it $from} {$it<=$to} {incr it} {
        set res [uplevel 1 expr $res+$body]
    }
    set res
 }
 proc fact n {expr {$n<2? 1: wide($n)*[fact [incr n -1]]}}

It worked alright (the wide() cast was necessary to enter the 64 bit realm), but in the 18th iteration got saturated into a slightly wrong result, while expr itself knows better:

 % Sum i 0 17 {1./[fact $i]}
 2.7182818284590455
 % expr exp(1)
 2.7182818284590451

---

Continued fraction edit

Also in the J paper, it is shown how to approximate the golden ratio x-1 = 1/x with the continued fraction

 (+ %) / 15 $ 1

which in more conventional spelling is

             1
 1 + ------------------
               1
     1 + --------------
                 1
         1 + ----------
              1 + ...

ad infinitum (or for a number of iterations at least, 15 in the example). To wrap this nicely in Tcl, I invented an extra notation where @ stands for "the whole thing again". Execution has to start from bottom right of course, with a default value of 1, and work its way up for the specified number of iterations:

 proc continuedFraction {body iterations} {
    regsub -all @ $body {$res} body
    set res 1
    for {set i 0} {$i<$iterations} {incr i} {
        set res [expr $body]
    }
    set res
 }
 % continuedFraction {1 + 1./@} 15
 1.6180344478216819

With increasing number of iterations, the results oscillate ever closer around one value, until from 38 up they don't change any more:

 % continuedFraction {1 + 1./@} 38
 1.6180339887498949

---