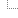12²⁰×e⁻¹²
p = ——————
20!
proc RandomPoisson {lambda count} {
#
# generate random numbers that are poisson distributed
#
# lambda -> expected value = "mean value" (which happens to also be the variance)
# count -> number of numbers to be generated
#
# (adapted from: "Parameter Estimation in Ecology" by O. Richter & D. Söndgerath)
# factorial f (here: the factorial of 0):
set f 1
# poisson probability of the value 0:
set su [expr {exp(-$lambda)}]
set p(0) $su
# probabilities of the integers up to the math limits of Tcl:
# (computed as the discrete density function)
set i 0
while {1} {
incr i
set f [expr {$f*$i}]
set su [expr {$su + exp(-$lambda) * pow($lambda,$i)/double($f)}]
if {$su > 1} {
# we cannot calculate more precisely here,
# so we assume 1 is ok for the final density:
set p($i) 1
break
}
set p($i) $su
}
# calculate random values according to the
# given discrete probability density function:
# (this does work for all dicrete distributions,
# not only for poisson)
for {set c 0} {$c < $count} {incr c} {
# random number in the interval [0,1]:
set x [expr {rand()}]
# transform this number to the correct target interval:
for {set j 0} {$j <= $i} {incr j} {
if {$p($j) > $x} {
lappend result $j
break
}
}
}
return $result
}We run into a problem here when using Tcl's normal expr. The numbers in the formula quickly put expr to its limits and therefore I have added the case where the probability is just set to 1, when this point arrives. You could use mpexpr instead if you need a better approximation of the very improbable part of the Poisson distribution.Here is a test: # produce 10,000 random integer numbers according to the Poisson distribution:
set data [RandomPoisson 3.5 10000]
# count their frequencies:
foreach el $data {
if {[info exists count($el)]} {
incr count($el) 1
} else {
set count($el) 1
}
}
# and display their frequencies:
foreach el [lsort -integer [array names count]] {
puts "$el => $count($el)"
}EKB This implements pdf-poisson (actually the Poisson has a probability mass function, pmf, but this matches the function names in tcllib), cdf-poisson, and random-poisson, which generates poisson-distributed random numbers. This version works efficiently for both small and large values of mu.From first version: The implementation of cdf-poisson does not seem particularly efficient, but it runs reasonably quickly even for large values. EKB: This is now fixed. It was reasonably fast, but couldn't handle large numbers. This version implements the cumulative distribution using the incomplete gamma function.
package require math
source "incgamma.tcl"
namespace eval poisson {}
proc poisson::random-poisson {mu number} {
if {$mu < 20} {
return [randp_invert $mu $number]
} else {
return [randp_PTRS $mu $number]
}
}
# Generate a poisson-distributed random deviate
# Use algorithm in section 4.9 of Dagpunar, J.S,
# "Simulation and Monte Carlo: With Applications
# in Finance and MCMC", pub. 2007 by Wiley
# This inverts the cdf using a "chop-down" search
# to avoid storing an extra intermediate value.
# It is only good for small mu.
proc poisson::randp_invert {mu number} {
set W0 [expr {exp(-$mu)}]
set retval {}
for {set i 0} {$i < $number} {incr i} {
set W $W0
set R [expr {rand()}]
set X 0
while {$R > $W} {
set R [expr {$R - $W}]
incr X
set W [expr {$W * $mu/double($X)}]
}
lappend retval $X
}
return $retval
}
# Generate a poisson-distributed random deviate
# Use the transformed rejection method with
# squeeze of Hoermann: Wolfgang
# Hoermann, "The Transformed Rejection Method
# for Generating Poisson Random Variables,"
# Preprint #2, Dept of Applied Statistics and
# Data Processing, Wirtshcaftsuniversitaet Wien,
# http://statistik.wu-wien.ac.at/
# This method works for mu >= 10.
# First, a helper proc
proc poisson::logfac {k} {
incr k
return [::math::ln_Gamma $k]
}
proc poisson::randp_PTRS {mu number} {
set smu [expr {sqrt($mu)}]
set b [expr {0.931 + 2.53 * $smu}]
set a [expr {-0.059 + 0.02483 * $b}]
set vr [expr {0.9277 - 3.6224/($b - 2.0)}]
set invalpha [expr {1.1239 + 1.1328/($b - 3.4)}]
set lnmu [expr {log($mu)}]
set retval {}
for {set i 0} {$i < $number} {incr i} {
while 1 {
set U [expr {rand() - 0.5}]
set V [expr {rand()}]
set us [expr {0.5 - abs($U)}]
set k [expr {int(floor((2.0 * $a/$us + $b) * $U + $mu + 0.43))}]
if {$us >= 0.07 && $V <= $vr} {
break
}
if {$k < 0} {
continue
}
if {$us < 0.013 && $V > $us} {
continue
}
if {log($V * $invalpha / ($a/($us * $us) + $b)) <= -$mu + $k * $lnmu - [logfac $k]} {
break
}
}
lappend retval $k
}
return $retval
}
proc poisson::pdf-poisson {mu k} {
set intk [expr {int($k)}]
expr {exp(-$mu + floor($k) * log($mu) - [logfac $intk])}
}
proc poisson::cdf-poisson {mu x} {
return [expr {1.0 - [incompleteGamma $mu [expr {floor($x) + 1}]]}]
}
##########################################################################################
##
## TESTING
##
## Can test pdf & cdf by running in a console. For random numbers, generate histograms:
##
##########################################################################################
package require math::statistics
canvas .c
pack .c -side top
frame .f
pack .f -side bottom
label .f.mul -text "mu"
entry .f.mue -textvariable mu
pack .f.mul -side left
pack .f.mue -side left
button .f.run -text "Run" -command runtest
pack .f.run -side left
proc runtest {} {
set numbins [expr {3 * $::mu}]
set vals [poisson::random-poisson $::mu 5000]
set remainder 5000
for {set x 0.0} {$x < $numbins} {set x [expr {$x + 1}]} {
lappend bins $x
set distval [poisson::pdf-poisson $::mu $x]
set distval [expr {int(5000 * $distval)}]
lappend distcounts $distval
}
# Assume none are left
lappend distcounts 0.0
set bincounts [::math::statistics::histogram $bins $vals]
.c delete hist
.c delete dist
math::statistics::plot-scale .c 0 $numbins 0 [math::statistics::max $bincounts]
math::statistics::plot-histogram .c $bincounts $bins hist
math::statistics::plot-histogram .c $distcounts $bins dist
.c itemconfigure dist -fill {} -outline green
}
console show
set mu 25
runtestEKB Using this library, here are some extensions on the example given at the top of the page. Suppose there is a site where on average 12 people visit per day. Also suppose that we're concerned with the possibility that we could have 20 people visit during a day. (This is a home-hosted site running an Atari (http://en.wikipedia.org/wiki/Atari_8-bit_family
 ) as the server :-) Then this snippet will find out a) the probability that exactly 20 people visit (the same as above); b) the probability that 20 or more visit:
) as the server :-) Then this snippet will find out a) the probability that exactly 20 people visit (the same as above); b) the probability that 20 or more visit: foreach cmd {{poisson::pdf-poisson 12 20} \
{expr 1 - [poisson::cdf-poisson 12 19]}} {
puts $cmd:
puts [eval $cmd]
puts ""
}And here are the results:poisson::pdf-poisson 12 20: 0.009682032170194331 expr 1 - [poisson::cdf-poisson 12 19]: 0.021279769383858338So, a 2.1% chance that we could be overloaded -- 2 days out of 100! Better upgrade the server! As an aside, these values agree well with the values calculated by R:
> dpois(20, 12) [1] 0.009682032 > 1-ppois(19,12) [1] 0.02127977Suppose also that this is a social networking site, and the load actually goes up as the square of the number of people. Now we're in real trouble. The question is, what is the average value of the square of the number of visitors, when the number is greater than or equal to 20? (OK, OK, I'm reaching here... it's just a demo!) This problem can be solved using Monte Carlo integration (see also A simple Monte Carlo simulation). Since this requires generating pseudo-random numbers, it is good to check how much variation there is between runs. This does three runs of 100,000 random variables each:
puts "Evaluate E(x^2 | x >= 20) using Monte Carlo integration:"
for {set i 1} {$i <= 3} {incr i} {
lassign {0 0} x2 n
set t [time {
foreach x [poisson::random-poisson 12 100000] {
if {$x >= 20} {
incr x2 [expr {$x * $x}]
incr n
}
}}]
regexp {^([0-9]+)} $t -> time
puts [format "Run %d (%0.1f sec): %f" $i [expr {1.0e-6 * $time}] \
[expr {double($x2)/double($n)}] \
]
}The core calculation is: foreach x [poisson::random-poisson 12 100000] {
if {$x >= 20} {
incr x2 [expr {$x * $x}]
incr n
}
}This generates a list of 100,000 Poisson-distributed random variates and, if they are greater than or equal to 20, adds the square of the value to a running sum and increments a count of values that were equal to or greater than 20. To calculate the average (or "expectation value," E()), of x^2 when x >= 20 -- E(x^2 | x >= 20) -- divide the sum of squares by the total number of values that were greater than or equal to 20. This is accomplished with the expression: expr {double($x2)/double($n)}Here's the output:Evaluate E(x^2 | x >= 20) using Monte Carlo integration: Run 1 (1.3 sec): 446.378132 Run 2 (1.4 sec): 447.252354 Run 3 (1.3 sec): 449.894809This may not be so bad. The value at 20 is 400, and the average of values above 20 is about 13% higher than this (450/400 = 1.125).(This problem can also be solved in closed form, but Monte Carlo is easier to get up and running.)